Pythonを使った音源処理
目 次
音源ファイル(ここではWAV(Waveform Audio File Format)ファイル)をpythonで周波数処理を行います。例として松ヶ崎キャンパスで録音した10秒程度の虫の鳴き声(bugs.wav)をバンドパスフィルタ処理します。
プログラムコードは以下に示しますが、実行環境は各自でGoogle ColaboratoryやVScode等を準備ください。
注意
実行時にライブラリが無い場合は適宜インストールしてください。
レポート作成時に今回の例であげた音源(虫の鳴き声(bugs.wav))は使えません。
まずはSonic Visualiserをインストールしてください。立ち上げ後、携帯電話で撮影した動画やマイクで録音した音源をドラッグアンドドロップでファイルを読み込みます。次にSonic Visualiserのメニューから下記を実行してpythonで処理する音源を用意したディレクトリにWAVファイルを保存してください。
使用 Sonic Visualiser (2024-06-19)
実行
File>Export Audio File...
|
サンプルコード
抽出した音源がステレオ音源かモノラル音源かどちらかわからないため、00_convert_to_monophonic_audio.pyでモノラル音源に変換します。
python .\00_convert_to_monophonic_audio.pyなどで実行してください。
実行時は入出力ファイル名の' '内を変えてください。
# Input and output files
input_audio_file = 'bugs.wav'
output_audio_file = 'bugs.wav'
サンプルコード 00_convert_to_monophonic_audio.py
import soundfile as sf
import numpy as np
# Input and output files
input_audio_file = 'bugs.wav'
output_audio_file = 'bugs.wav'
# Read the audio file
audio_data, samplerate = sf.read(input_audio_file)
# Determine if the audio is mono or stereo
if audio_data.ndim == 2:
# If stereo, convert to mono by averaging the left and right channels
mono_data = np.mean(audio_data, axis=1)
else:
# If already mono, use the data as is
mono_data = audio_data
# Write the mono audio to a new file
sf.write(output_audio_file, mono_data, samplerate)
最初は音源の時系列データを確認しましょう。図1のように背景雑音に鈴虫の鳴き声が埋もれていることが分かります。図1にFFT処理を行って図2のスペクトル分布を示します。3000 Hzから6000 Hzに鳴き声があり、背景は3000 Hz以下と読み取れます。
サンプルコード
図をプログラム(01_plot_wav_sound.py)で描画しましょう。各自の環境に合わせて入出力ファイル名はinput_audio_fileとoutput_image_fileの" "内を変更してください。
python .\01_plot_wav_sound.py、python .\02_plot_wav_spectrum.pyとコマンド実行すると確認出来ます。

図1:音源の時系列データ
|

図2:音源のスペクトル分布
|
サンプルコード 01_plot_wav_sound.py
import soundfile as sf
import numpy as np
import matplotlib.pyplot as plt
# Input and output files
# Input and output files
input_audio_file = "bugs.wav"
output_image_file = 'Fig.1_bugs.png'
# Load the wav file using soundfile
audio_data, samplerate = sf.read(input_audio_file)
# Remove DC offset by subtracting the mean
audio_data = audio_data - np.mean(audio_data)
# Generate time axis
time = np.linspace(0, (len(audio_data) - 1) / samplerate, num=len(audio_data))
# Plot the audio data
plt.figure(figsize=(12, 6))
plt.plot(time, audio_data)
plt.title('Time Series Audio Data')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.grid(True)
# Save the plot as a PNG image
plt.savefig(output_image_file)
# Display the plot
# plt.show()
サンプルコード 02_plot_wav_spectrum.py
import soundfile as sf
import numpy as np
import matplotlib.pyplot as plt
# Input and output files
input_audio_file = "bugs.wav"
output_image_file = 'Fig.2_spectrum.png'
# Load the wav file using soundfile
audio_data, samplerate = sf.read(input_audio_file)
# Remove DC offset by subtracting the mean
audio_data = audio_data - np.mean(audio_data)
# Perform Fourier transform
frequencies = np.fft.rfftfreq(len(audio_data), d=1/samplerate)
spectrum = np.abs(np.fft.rfft(audio_data))
# Plot the spectrum
plt.figure(figsize=(12, 6))
plt.plot(frequencies, spectrum)
plt.title('Spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.grid(True)
# Save the plot as a PNG image
plt.savefig(output_image_file)
# Display the plot
# plt.show()
図2のスペクトルから鳴き声の周波数帯を推測しましたが、時系列の情報と各時刻付近でのスペクトルがわかるともっと理解しやすいです。
そこで、図3のように同時に表示できるスペクトログラムでその特徴を確認します。図2ではわからなかった特徴として、3000 Hzから4000 HZ帯では継続的な鳴き声があり、
4500 Hzから6000 Hz帯で断続的な鳴き声があることがわかります。また3000 Hz以下でおそらく室外機などから発生する背景雑音は、
継続的な波形を持つことが分かります。
サンプルコード
input_audio_fileとoutput_image_fileで入出力ファイル名を変更できます。

図3:鈴虫の鳴き声のスペクトログラム
|
サンプルコード 02_plot_wav_spectrogram.py
import soundfile as sf
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import spectrogram
# Input and output files
input_audio_file = "bugs.wav"
output_image_file = 'Fig.3_spectrogram.png'
# Load the wav file using soundfile
audio_data, samplerate = sf.read(input_audio_file)
# Remove DC offset by subtracting the mean
audio_data = audio_data - np.mean(audio_data)
# Compute the spectrogram
frequencies, times, Sxx = spectrogram(audio_data, samplerate)
# Add a small value to Sxx to avoid log10(0)
Sxx += 1e-10
# Plot the spectrogram
plt.figure(figsize=(12, 6))
plt.pcolormesh(times, frequencies, 10 * np.log10(Sxx), shading='gouraud')
plt.title('Spectrogram')
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.colorbar(label='Intensity (dB)')
plt.ylim(0, 8000) # Adjust the frequency range for better visibility
# Save the plot as a PNG image
plt.savefig(output_image_file)
# Display the plot
#plt.show()
虫の鳴き声(bugs.wav)を,図3から推定した3000 Hzから6000 Hzの帯域でバンドパスフィルタを適用した結果が、
図4のようなグラフで表示される音源(filtered_bugs.wav)になりました。如何でしょうか?室外機などの低周波成分
が無くなり、鈴虫の鳴き声だけがよく聞き取ることができました。図4は既出コードで描画しましょう。
サンプルコード
03_band_pass_wav.pyなどで保存して,python .\03_band_pass_wav.pyとコマンド実行すると確認出来ます。帯域はlowcutとhighcutに入力する値を変えてください。
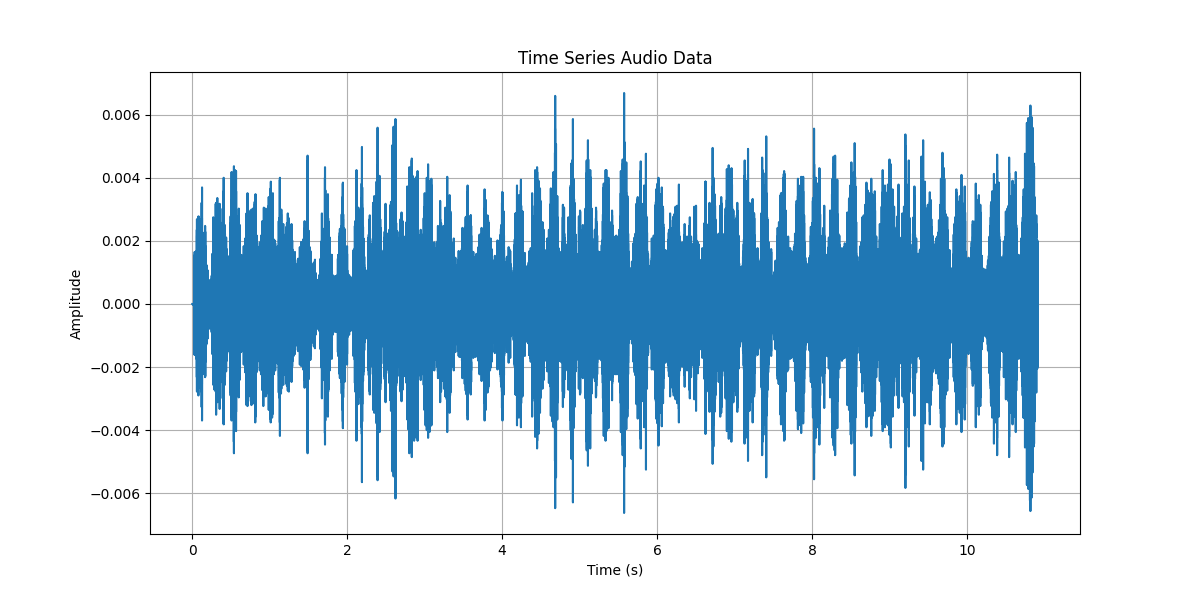
図4:処理後の鈴虫の鳴き声のスペクトログラム
|
サンプルコード 03_band_pass_wav.py
import soundfile as sf
import numpy as np
from scipy.signal import butter, filtfilt
# Input and output files
input_audio_file = "bugs.wav"
output_audio_file = 'filtered_bugs.wav'
# Range of a bandpass filter from lowcut Hz to highcut Hz
lowcut = 3000.0
highcut = 6000.0
# Load the wav file using soundfile
audio_data, samplerate = sf.read(input_audio_file)
# Remove DC offset by subtracting the mean
audio_data = audio_data - np.mean(audio_data)
# Parameters of a bandpass filter with Butterworth filter
nyquist = 0.5 * samplerate
low = lowcut / nyquist
high = highcut / nyquist
b, a = butter(N=4, Wn=[low, high], btype='band')
# Apply the bandpass filter to the audio data
filtered_audio_data = filtfilt(b, a, audio_data)
# Save the filtered audio to a new wav file
sf.write(output_audio_file, filtered_audio_data, samplerate)
最後に処理音源のスペクトル分布とスペクトログラムを図4と図5で確認します。図2と図4を比べると、指定通りの帯域のみ振幅分布がみられますがその他は0になって、フィルターの適用を確認出来ました。
同様に図3と図5を比べると、バンドパスフィルタの適用を確認することが出来ます。
原音源(bugs.wav)は信号と雑音の周波数帯が重なっていないため、処理音源(filtered_bugs.wav)からわかるようにバンドパスフィルタの適用がうまく行きました。重なっている場合は、Spectral subtraction法やWiener filterなど別の方法を試してください。いろいろな方法があり非常に奥深く楽しいです。
実行例
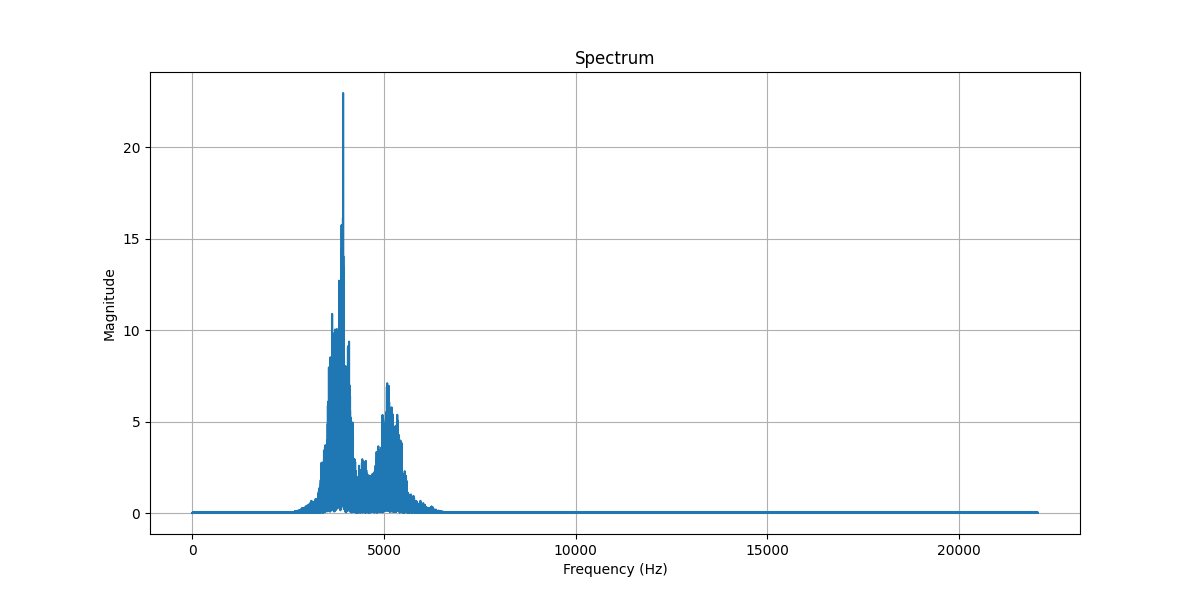
図4:処理音源のスペクトル分布
|
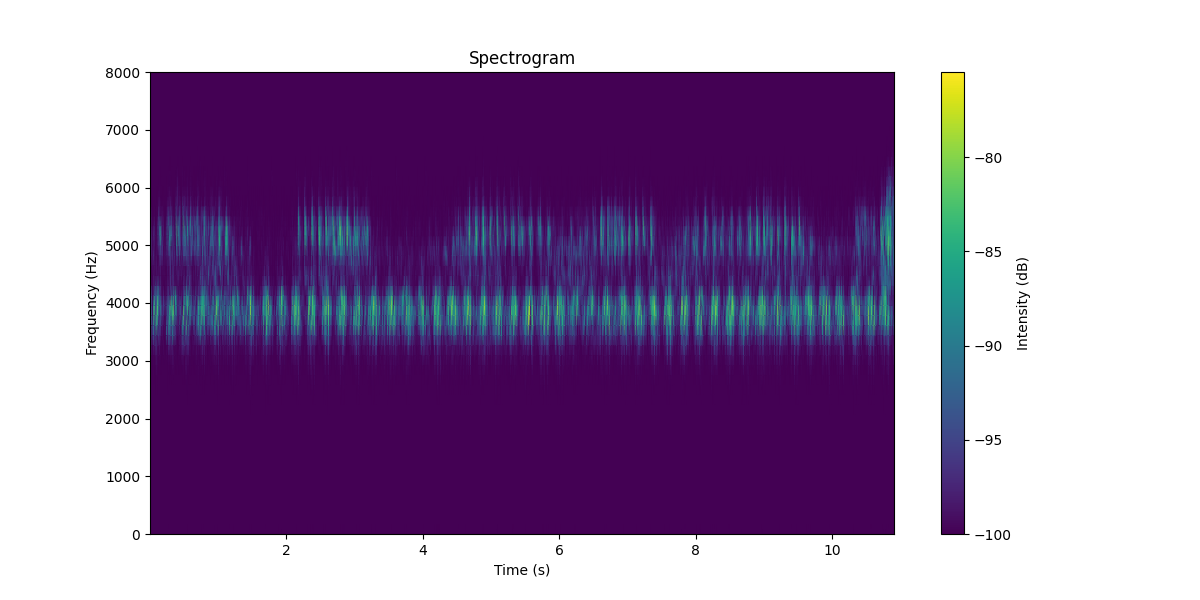
図5:処理音源のスペクトログラム
|
© Measurement System Laboratory, Kyoto Institute of Technology.

| 






